Prelude of the Chambered, a game by Notch.

It took Notch 48 hours to make this fully playable game from scratch. I can’t play it right now because I’m at work, but I’ll beat it tonight!

It’s amazing because yesterday night I re-installed my old Might and Magic 3 to have a feel of old-school 3D. Prelude of the Chambered is more on the Wolfenstein side, but that’s a perfect timing.

Here, have a glimpse of how a real coder (not me) works:

Youtube link: Creating Prelude of the Chambered.

It should be quite possible to render Infiniworld with such a 3D engine.  It’s actually one of my goals for Infiniworld 2 or 3 :].

Edit, later that evening:

I died, I was so close! I got lost on my way back from the temple, the ghost boss running after me while I had only 4 health points left. Now I’m scared.

No save/reload buttons, like in real life :(.

Collision response.

Urgh, the night was too short but I had to wake up early otherwise I’ll be a zombie tomorrow Monday.

Since my last post, we are experts in detecting collisions in our super simplistic universe.  It is time to react to it.

I can see two things to do:

1. We must correct the position of the entity to put it in a legit place, that is a place where it does not collide anything.
2. We must transfer energy between the collider and the collidee, including some loss to simulate friction in deformable bodies.  This changes velocities.

Position correction.

The simple case.

Figure 1: Correction of the position of a circle colliding with an edge.

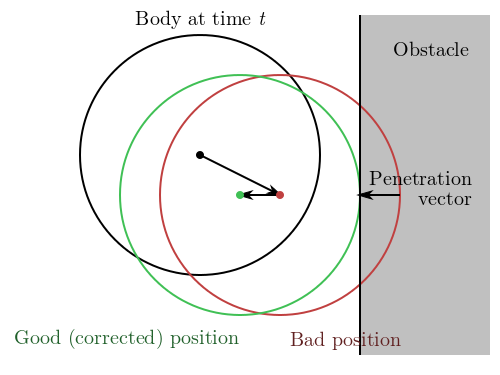
Since we’re doing science here, I started giving numbers to my figures.  See Figure 1.  On this figure, the arrows do not represent speeds, they represent translation (movement, displacement) vectors.

1. An entity (circle) is at position Black.
2. We integrate its motion.
3. The motion integrator says that after the time step, the entity should be in the Red position.
4. Our collision detector notices that the Red circle intersects the edge of an obstacle (the gray thing).  We must respond to this collision.
5. We measure how much the entity penetrated the obstacle: we get a penetration vector.
6. We add the penetration vector to the Red position to get the Green position.  That’s where out entity ends up.

Doing it that way has an advantage: when you hit a wall you don’t get stuck on it but you start sliding.  We see that behavior in many games, now you know how it is done.

The correction algorithm is identical for collisions with circles and corners, only the detection changes.  Actually, a corner is a circle with a radius of 0, I can use the same code.

Chained collisions.

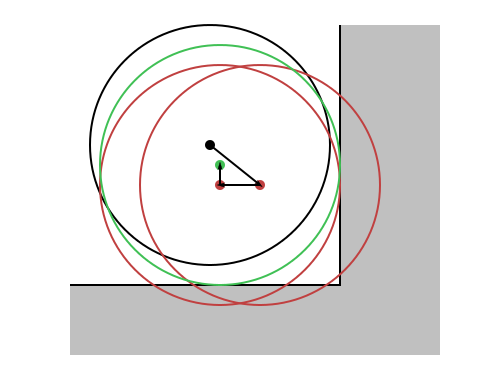
Now, what if Green is also a bad position?  See figure 2.  Well, Green becomes the new Red, and we start again at the step number 4.  We keep doing that until we stop being in wrong places.  Just to make sure we don’t get stuck in an endless loop, I will authorize a maximum of, let’s say, 5 such attempts.  After that, I cancel the whole movement and the entity is sent back to the Black position.  5 is an arbitrary number, maybe there is a better one ; I will log something in the console when this number is exceeded so that I can see the situations where things are going wrong.  Maybe I will come up with a better algorithm to solve these situations.

Figure 2: chain of position corrections.

Simultaneous collisions.

Let’s look at figure 2 again.  The first red circle intersects two edges simultaneously.  We reacted by correcting for the closest collision first.  Indeed, we hit the right wall before the bottom wall so it makes sense to react to these collisions that way.  We ordered collisions by distances.

But maybe we could also correct all these collisions at the same time instead of going back to step 4 (detecting the new closest collision).  Since each collision comes with a penetration vector, we just add them all and we get our Green position immediately.  Only after correcting for all these collisions we go back to step 4.  Indeed, maybe something else that we didn’t notice with our first Red position is in the way now.  Look at Figure 3.

Figure 3: Same as Figure 2, but a small entity intersects Green.

Figure 3 shows a small entity with which we did not collide after our integration.  We corrected for the two walls and we got the Green position, but now we have to test Green for collisions again otherwise we miss the small entity.  GOTO 4.

Velocity correction.

Elastic collision.

We are going to implement elastic collisions.  You have an elastic collision when, after the collision, the energy and the momentum of the system are the same than before.

Figure 4: Elastic collisions.

Picture 4 shows a frontal collision, but our collisions won’t always be frontal.  See figure 5 for an illustration.

Figure 5: geometry of a collision. Only the normal component of the velocities is modified by the elastic collision.

When two bodies collide, there are two preferred axis for describing the collision: the normal and the tangent axis.  If the velocities of the two bodies were collinear to the normal axis, then the collision would be frontal.  In any case, only the normal component of the velocities is modified during an elastic collision.  So the first thing we must do is decompose the velocities, which reduces our problem from vector to scalar.  Then we can use the formulas from the wikipedia page to exchange the energy.  Finally we rebuild the vectors.

Energy dissipation, efficiencies.

Unless you are made of rubber or super hard metal, there is very little chance that you bounce back when you hit a wall.  We can introduce here two efficiencies: one for the normal component and one for the tangential component.  These efficiencies should be between 0 and 1.  After applying the formulas for the elastic collision, we multiply our four scalars (two per velocity times two velocities) by these efficiencies.  A very high normal efficiency such as 0.95 could simulate the very low loss of energy or a bouncing rubber ball.  A lower efficiency such as 0.50 could simulate what happens to you when you run into a wall.

The efficiencies are functions of the material.  The two bodies have a priori different materials and their efficiencies are multiplied.  If a rubber ball (0.95) bounces pretty well on a stone wall (0.99) with a combined efficiency of 0.95 * 0.99 = 0.94, the same rubber ball does not bounce well at all on you (0.50) since the combined efficiency is 0.99 * 0.50 = 0.49.

It is easy to understand the normal efficiency: it tells you how bouncy the material is.  The tangential efficiency is weirder, maybe it can simulate some kind of friction.

The order of the collisions.

When we are computing the collision response for the velocities, we cannot do what we did for the positions.  For the position correction, we applied all the corrections for all the detected collisions at once.  With velocities, the order of the collisions matters.  We run the dissipative elastic collision code on all the detected collisions, one by one, starting with the closest one.

Actually, if we were trying to be super precise, we could imagine that after our collision on the right wall of Figure 2 we lost so much speed that we won’t collide with the other wall.  There is no way we implement that: doing so would require to find the exact time of the first collision then restart our integration from there with the corrected velocity.  We are not going for something that precise; instead, we will consider that somehow we did collide with all that, and at the very end we’ll see if we have some speed left.  Remember, it all happens within a twentieth of a second (the period of our physics engine).

We have another problem: what if we collide two things at the same time?  The two collisions are at the same distance, so we should compute an elastic collision of three bodies.  It could even be worse, with four or five bodies…  That’s many variables and only two equations (conservation of energy and conservation of mass).  I could group bodies together and replace them by their center of mass but I declare that “too complicated for now”.  I will just apply the collisions one after another, essentially randomly.  We are dealing with distances that are way smaller than a pixel here, and we are represented by circles but we are not circles, so let’s not over-design a simplification.

Let’s start coding then!

That should work, right?  Something tells me this won’t be done by Monday :).